Question

Two vectors are given by a = 8.6i + 5.1 j and b = 931 + 9.5.

Find
(a). [a xb]
(b). a.b ,
(c) a + b . b , and
(d) the component of a along the direction of b.

Answer 1

Assuming b = 9.3i + 9.5j (b = 931 + 9.5 is wrong):

a) a×b = 34.27k

b) a·b = 128.43

c) (a + b)·b = 305.17

d) The component of a along the direction of b = 9.66

Step-by-step explanation:

Assuming b = 9.3i + 9.5j (b = 931 + 9.5 is wrong) we can proceed as follows:

a) The vectorial product, a×b is:

`a * b = (8.6*9.5 - 5.1*9.3)k = 34.27k`

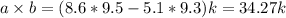
b) The escalar product a·b is:

`a\cdot b = (8.6*9.3) + (5.1*9.5) = 128.43`

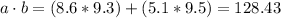
c) Asumming (a + b)·b instead a+b·b we have:

`(a + b)\cdot b = [(8.6 + 9.3)i + (5.1 + 9.5)j]\cdot (9.3i + 9.5j) = (17.9i + 14.6j)\cdot (9.3i + 9.5j) = 305.17`

d) The component of a along the direction of b is:

`a*cos(\theta) = (a\cdot b)/(|b|) = \frac{128.43}{\sqrt{9.3^(2) + 9.5^(2)}} = 9.66`

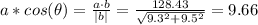
I hope it helps you!