Answer:
The product of two rational numbers is rational, and the sum of two rational numbers is irrational.
Explanation:
Let be
 and
and
 rational numbers whose forms are, respectively:
rational numbers whose forms are, respectively:
 and
and
 ,
,
 ,
,
 ,
,
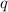 ,
,


We proceed to demonstrate if the Pythagorean sum of two rational numbers leads to a rational number.
1)
 ,
,
 ,
,
 ,
,
 ,
,
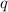 ,
,

 Given.
Given.
2)
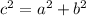 Given.
Given.
3)
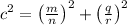 1) in 2)
1) in 2)
4)
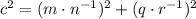 Definition of division.
Definition of division.
5)
![c^(2) = [m^(2)\cdot (n^(-1))^(2)]+[q^(2)\cdot (r^(-1))^(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/rme1y4lh23xq6m3ya9paadp6cgbxvgafxw.png)
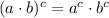
6)
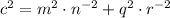
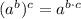
7)
![c^(2) = [m^(2)\cdot (n^(2))^(-1)]+[q^(2)\cdot (r^(2))^(-1)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/v3jxw95m0goc2zldrfsg3ptso1984q8zjh.png)
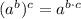
8)
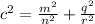 Definition of division.
Definition of division.
9)

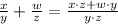
10)
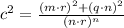
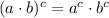 /Result.
/Result.
If
 is a rational number, then
is a rational number, then
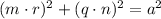 , so that
, so that
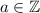 . Which means that
. Which means that
 will be rational number if and only if the square root of
will be rational number if and only if the square root of
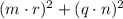 is an entire number.
is an entire number.
Which means that correct answer is B.