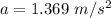Question

An engineer in a locomotive sees a car stuck on the track at a railroad crossing in front of the train. When the engineer first sees the car, the locomotive is 260 m from the crossing and its speed is 26 m/s. If the engineer's reaction time is 0.51 s, what should be the magnitude of the minimum deceleration to avoid an accident? Answer in units of m/s 2

Answer 1

The right answer is "1.369 m/s²".

Step-by-step explanation:

The given values are:

Distance (s)

= 260 m

Initial speed (u)

= 26 m/s

Reaction time (t')

= 0.51 s

During reaction time, the distance travelled by locomotive will be:

⇒
`s'=ut'`

`=26* 0.51`

`=13.26 \ m`

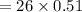
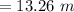
Remained distance between locomotive and car:

⇒
`x=s-s'`

`=260-13.26`

`=246.74 \ m`

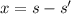
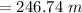
Now,

The final velocity to avoid collection is, V = 0 m/s

From third equation of motion:

⇒
`V^2=u^2+2ax`

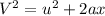
On putting the estimated values, we get

⇒
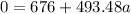
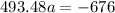
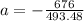
`0=(26)^2+2* a* 246.74`

⇒
`0=676+493.48a`

⇒
`493.48a=-676`

⇒
`a=-(676)/(493.48)`

⇒
`a=1.369 \ m/s^2`