Question

A coaxial cable has a charged inner conductor (with charge +8.5 µC and radius 1.304 mm) and a surrounding oppositely charged conductor (with charge −8.5 µC and radius 9.249 mm).

Required:
What is the magnitude of the electric field halfway between the two cylindrical conductors? The Coulomb constant is 8.98755 × 10^9 N.m^2 . Assume the region between the conductors is air, and neglect end effects. Answer in units of V/m.

Answer 1

Complete question:

A 50 m length of coaxial cable has a charged inner conductor (with charge +8.5 µC and radius 1.304 mm) and a surrounding oppositely charged conductor (with charge −8.5 µC and radius 9.249 mm).

Required:

What is the magnitude of the electric field halfway between the two cylindrical conductors? The Coulomb constant is 8.98755 × 10^9 N.m^2 . Assume the region between the conductors is air, and neglect end effects. Answer in units of V/m.

Answer:

The magnitude of the electric field halfway between the two cylindrical conductors is 5.793 x 10⁵ V/m

Step-by-step explanation:

Given;

charge of the coaxial capable, Q = 8.5 µC = 8.5 x 10⁻⁶ C

length of the conductor, L = 50 m

inner radius, r₁ = 1.304 mm

outer radius, r₂ = 9.249 mm

The magnitude of the electric field halfway between the two cylindrical conductors is given by;

`E = (\lambda)/(2\pi \epsilon_o r) = (Q)/(2\pi \epsilon_o r L)`

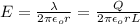
Where;

λ is linear charge density or charge per unit length

r is the distance halfway between the two cylindrical conductors

`r = r_1 + (1)/(2)(r_2-r_1) \\\\r = 1.304 \ mm \ + \ (1)/(2)(9.249 \ mm-1.304 \ mm)\\\\r = 1.304 \ mm \ + \ 3.9725 \ mm\\\\r = 5.2765 \ mm`

The magnitude of the electric field is now given as;

`E = (8.5*10^(-6))/(2\pi(8.85*10^(-12))(5.2765*10^(-3))(50)) \\\\E = 5.793*10^5 \ V/m`

Therefore, the magnitude of the electric field halfway between the two cylindrical conductors is 5.793 x 10⁵ V/m