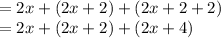Explanation:
We are to get the expression for the following statements;
1) The difference of nine times a number x and the quotient of that number and 5.
The product of nine and a number x is expressed as;
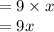
The quotient of that number and 5.
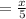
The difference between both expression;
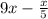
Hence, the difference of nine times a number x and the quotient of that number and 5 is expressed as
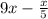
2) Eight more than the quotient of twelve and a number n
Quotient of twelve and a number n is expressed as:

Eight more than the resulting function is;
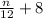
Hence eight more than the quotient of twelve and a number n is expressed as
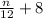
3) The product of a number and the quantity 'six minus the number' plus the quotient of eight and the number.
Let the number be x:
six minus the number is expressed as;
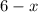
product of a number x and the quantity 'six minus the number is;
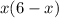
quotient of eight and the number is;

Taking the resulting sum of the last two expression
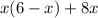
Hence the product of a number and the quantity 'six minus the number' plus the quotient of eight and the number is expressed as;
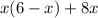
4) Sum of three consecutive even integers. 2x + (2x + 2) + (2x + 4).
Let the first even number be 2x
The consecutive even numbers are gotten by adding 2 to the preceding number. The two consecutive even integers are 2x+2 and 2x+2+2
the sum of three consecutive even integers is expressed as;