Answer:
El ángulo apropiado de lanzamiento para la bala de cañón es aproximadamente 61.60º.
Step-by-step explanation:
(La figura asociada al enunciado ha sido adjuntado a esta solución)
De la Física Mecánica comprendemos que la trayectoria de la bala de cañón puede representarse como un tiro parabólico, esto es, la combinación de un movimiento horizontal a velocidad constante y un movimiento vertical en caída libre, esto es, uniformemente acelerado por la gravedad terrestre. Supongamos
El propósito de este problema consiste en determinar el ángulo de lanzamiento tal que la bala no toque la loma. Las ecuaciones de movimiento de la bala de cañón son las siguientes:
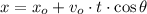 (Ec. 1)
(Ec. 1)
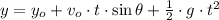 (Ec. 2)
(Ec. 2)
Where:
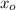 ,
,
 - Posiciones horizontales inicial y actual, medidas en metros.
- Posiciones horizontales inicial y actual, medidas en metros.
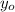 ,
,
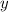 - Posiciones verticales inicial y actual, medidas en metros.
- Posiciones verticales inicial y actual, medidas en metros.
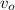 - Velocidad inicial, medida en metros por segundo.
- Velocidad inicial, medida en metros por segundo.
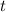 - Tiempo, medido en segundos.
- Tiempo, medido en segundos.
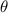 - Ángulo de lanzamiento, medido en grados sexagesimales.
- Ángulo de lanzamiento, medido en grados sexagesimales.
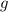 - Aceleración gravitacional, medida en metros por segundo al cuadrado.
- Aceleración gravitacional, medida en metros por segundo al cuadrado.
Si sabemos que
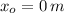 ,
,
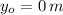 ,
,
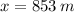 ,
,
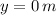 ,
,
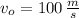 ,
,
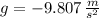 , obtenemos el siguiente sistema de ecuaciones:
, obtenemos el siguiente sistema de ecuaciones:
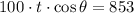 (Ec. 1b)
(Ec. 1b)
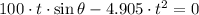 (Ec. 2b)
(Ec. 2b)
Aplicando la identidad trigonométrica fundamental (
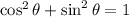 ) y algo de manipulación algebraica, podemos encontrar el tiempo requerido por la bala de cañón:
) y algo de manipulación algebraica, podemos encontrar el tiempo requerido por la bala de cañón:
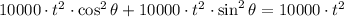 (Ec. 3)
(Ec. 3)
De (Ecs. 1b y 2b) en (Ec. 3):
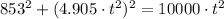
Y encontramos este polinomio de cuarto grado:
 (Ec. 4)
(Ec. 4)
Las raíces de este polinomio pueden calcularse analíticamente por la Fórmula de la Cuadrática, en tanto que la expresión es un caso especial que lo admite:
 ,
,
 ,
,
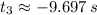 ,
,
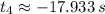
Físicamente hablando, las dos primeras raíces parecen razonables. Complementamos este resultado con el gráfico correspondiente a la función. Estos tiempos estarían relacionados con dos ángulos de tiro distintos, los cuales se determinan a partir de (Ec. 1b):
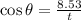
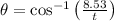
(i)
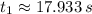
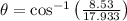
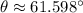
(ii)
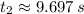
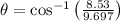
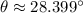
La altura de la loma es un criterio para descartar los ángulos de tiro inconvenientes, estos son, aquellos disparos que impactarían en la loma, se utilizan las siguientes ecuaciones de movimiento:
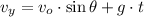 (Ec. 5)
(Ec. 5)
Encontramos las velocidades a máxima altura:
(i)
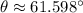 ,
,
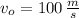 ,
,
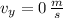 ,
,
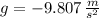 :
:
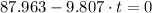
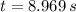
(ii)
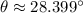 ,
,
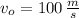 ,
,
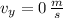 ,
,
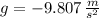 :
:
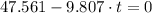
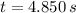
Finalmente, encontramos las alturas máximas respectivas de cada tiro:
(i)
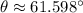 ,
,
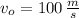 ,
,
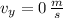 ,
,
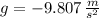 ,
,
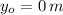 ,
,
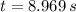 :
:
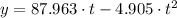
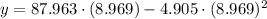
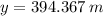
(ii)
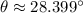 ,
,
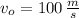 ,
,
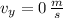 ,
,
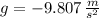 ,
,
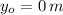 ,
,
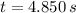 :
:
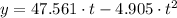
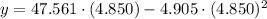
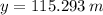
En consecuencia, el ángulo apropiado de lanzamiento para la bala de cañón es aproximadamente 61.60º.