Question

You are a member of a geological team in Central Africa. Your team comes upon a wide river that is flowing east. You must determine the width of the river and the current speed (the speed of the water relative to the earth). You have a small boat with an outboard motor. By measuring the time it takes to cross a pond where the water isn’t flowing, you have calibrated the throttle settings to the speed of the boat in still water. You set the throttle so that the speed of the boat relative to the river is a constant 6.00 m/s. Traveling due north across the river, you reach the opposite bank in 20.1s. For the return trip, you change the throttle setting so that the speed of the boat relative to the water is 9.00 m/s. You travel due south from one bank to the other and cross the river in 11.2 s.

Required:
a. How wide is the river, and what is the current speed?
b. With the throttle set so that the speed of the boat relative to the water is 6.00 m/s, what is the shortest time in which you could cross the river, and where on the far bank would you land?

Answer 1

(a). The width of the river is 90.5 m.

The current speed of the river is 3.96 m.

(b). The shortest time is 15.0 sec and we would end 59.4 m east of our starting point.

Step-by-step explanation:

Given that,

Constant speed = 6.00 m/s

Time = 20.1 sec

Speed = 9.00 m/s

Time = 11.2 sec

We need to write a equation for to travel due north across the river,

Using equation for north

`v^2-c^2=(w^2)/(t^2)`

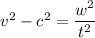
Put the value in the equation

`6.00^2-c^2=(w^2)/((20.1)^2)`

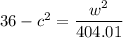`36-c^2=(w^2)/(404.01)`....(I)

We need to write a equation for to travel due south across the river,

Using equation for south

`v^2-c^2=(w^2)/(t^2)`

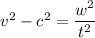
Put the value in the equation

`9.00^2-c^2=(w^2)/((11.2)^2)`

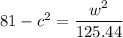`81-c^2=(w^2)/(125.44)`....(II)

(a). We need to calculate the wide of the river

Using equation (I) and (II)

`45=(w^2)/(125.44)-(w^2)/(404.01)`

`45=w^2(0.00549)`

`w^2=(45)/(0.00549)`

`w=\sqrt{(45)/(0.00549)}`

`w=90.5`

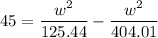
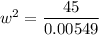
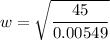
We need to calculate the current speed

Using equation (I)

`36-c^2=((90.5)^2)/((20.1)^2)`

`36-c^2=20.27`

`c^2=20.27-36`

`c=√(15.73)`

`c=3.96\ m/s`

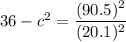
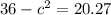
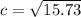
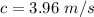
(b). We need to calculate the shortest time

Using formula of time

`t=(d)/(v)`

`t=(90.5)/(6)`

`t=15.0\ sec`

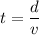
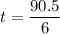
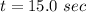
We need to calculate the distance

Using formula of distance

`d=vt`

`d=3.96*15.0`

`d=59.4\ m`

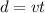
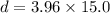
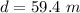
Hence, (a). The width of the river is 90.5 m.

The current speed of the river is 3.96 m.

(b). The shortest time is 15.0 sec and we would end 59.4 m east of our starting point.