Question

Consider a capacitor made of two rectangular metal plates of length and width , with a very small gap between the plates. There is a charge on one plate and a charge on the other. Assume that the electric field is nearly uniform throughout the gap region and negligibly small outside. Calculate the attractive force that one plate exerts on the other. Remember that one of the plates doesn't exert a net force on itself. (Enter the magnitude. Use any variable or symbol stated above along with the following as necessary: r0.)

F = θ/2∑0_w

Answer 1

F= σ² L² /2ε₀

F = (L² ε₀/4π) ΔV² / r⁴

Step-by-step explanation:

a) For this exercise we can use Coulomb's law

F = - k Q² / r²

where the negative sign indicates that the force is attractive and the value of the charge is equal to the two plates

Capacitance is defined by

C = Q / ΔV

Q = C ΔV

also the capacitance for a parallel plate capacitor is related to its shape

C = ε₀ A / r

we substitute

Q = ε₀ A ΔV / r

we substitute in the force equation

F = k (ε₀ A ΔV / r)² / r²

k = 1 / 4πε₀

F = ε₀ /4π L² ΔV² / r⁴4

F = L² ΔV² ε₀/ (4π r⁴)

F = (L² ε₀/4π) ΔV² / r⁴

b) Another way to solve the exercise is to use the relationship between the force and the electric field

F = q E

where we can calculate the field created by a plane using Gaussian law, where we use a cylinder with a base parallel to the plate as the Gaussian surface

Ф = ∫E .dA =
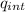`q_(int)` / ε₀

the plate have two side

2E A = q_{int} / ε₀

E = σ / 2ε₀

σ = q_{int} / A

substituting in force

F = q σ / 2ε₀

the charge total on the other plate is

q = σ A

q = σ L²

F= σ² L² /2ε₀