Question

You have just opened a new nightclub, Russ' Techno Pitstop, but are unsure of how high to set the cover charge (entrance fee). One week you charged $7 per guest and averaged 345 guests per night. The next week you charged $10 per guest and averaged 300 guests per night.

(a) Find a linear demand equation showing the number of guests q per night as a function of the cover charge p. q(p) =

(b) Find the nightly revenue R as a function of the cover charge p. R(p) =

(c) The club will provide two free non-alcoholic drinks for each guest, costing the club $2 per head. In addition, the nightly overheads (rent, salaries, dancers, DJ, etc.) amount to $2,000. Find the cost C as a function of the cover charge p. C(p) =

(d) Now find the profit in terms of the cover charge p. P(p) = Determine the entrance fee you should charge for a maximum profit. p = $ per guest

Answer 1

(a) The number of guest per night=p,

and the cover charge for one night per person=q.

Let the liner demand equation be
`q(p)=mp+c\cdots(i)`,

where m and c are constants.

Given that for the first week: q=345 and p=$7 and

for the second night: q=300 and p=$10.

Put these values in equation (i), we have

345=7m+c

`\Rigntarrow c=345-7m\cdots(ii)`

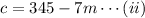
and

300=10m+c

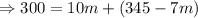`\Rightarrow 300=10m+(345-7m)` [from equation (ii)]

`\Rightarrow 3m=-45`

`\Rightarrow m=-15`

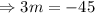
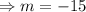
and from equation (ii),

`c=345-7*(-15)=450`.

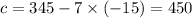Hence, the required demand equation is:

`q(p)=-15p+450\cdots(iii)`

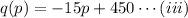
(b) Revenue = (Number of guests) x (Cover charge)

R=qp

`\Rightarrow R(p)=(-15p+450)p` [from equation (iii)]

`\Rightarrow R(p)=-15p^2+450p\;\cdots(iv)`

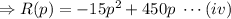
(c) The costs per night for drinks for the number of guest p is $2p and the nightly overheads is $2000.

So, the required cost function is

`C(p)=2p+2000\;\cdots(v)`

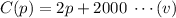
(d) Profit=(Revenue)-(Total costs)

i.e
`P(p)=R(p)-C(p)`

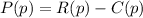
Using equations (iv) and (v), we have

`\Rightarrow P(p)=(-15p^2+450p)-(2p+2000)`

`\Rightarrow P(p)=-15p^2+448p-2000.`

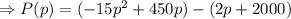
Now we have the profit function as function of cover charge (entry fee) per person.

So, to get the maximum profit, P, differentiate the profit function with respect to the cover charge, q and equate it to zero to get the eqtremum point.

`\frac {dP}{dq}=0`

`\Rightarrow -30p+448=0`

`\Rightarrow p=14.93`

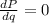
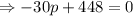
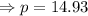
This point is either maxima or minima, so differentiate the profit function twice to to ensure the value of p corrosponding to what.

`\frac {d^2P}{dq^2}=-30`

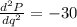
This the second deravitive is negative, so p=14.93 is the value for maximum profit.

Hence, for the maximum profit, the cover charge per guest is $14.93.