Question

2.Use the following graph to estimate the rate of change of the function at x=0.5 using the points (−1,−1) and (1,3)

A.The rate of change is −1/2.

B.The rate of change is 2.

C.The rate of change is 1/2.

D.The rate of change is −2.

3.The following graph shows the inches of snow on the ground over a certain number of hours. Use the graph to estimate the rate of change of the function at 3 hours using the points (0,0) and (5,10)

A.The rate of change is −1/2 of an inch per hour.

B.The rate of change is 1/2 of an inch per hour.

C.The rate of change is 2 inches per hour.

D.The rate of change is −2 inches per hour.

4.The following graph shows the average temperatures in degrees Fahrenheit (°F) over the days of a month. Use the graph to estimate the rate of change of the function at the ninth day of the month using the points (2,55) and (10,65)

A.The rate of change is 0.8 degrees Fahrenheit per day.

B.The rate of change is 1.25 degrees Fahrenheit per day.

C.The rate of change is −0.8 degrees Fahrenheit per day.

D.The rate of change is −1.25 degrees Fahrenheit per day.

5.Use the following graph to answer which of the following points would provide the most accurate estimation for the rate of change of the function as it crosses the y-axis. Explain.

(−0.5, 2)

(0.5, 3)

(−0.5, 3)

(0.5, 1)

A.(−0.5, 3) and (0.5, 1) would provide the most accurate estimation. The slope of the line drawn between these two points appears closest to the slope of the function at x=0.

B.(−0.5, 2) and (0.5, 3) would provide the most accurate estimation. The slope of the line drawn between these two points appears closest to the opposite of the slope of the function at x=0.

C.(−0.5, 2) and (0.5, 3) would provide the most accurate estimation. The slope of the line drawn between these two points appears closest to the slope of the function at x=0.

D.(−0.5, 3) and (0.5, 1) would provide the most accurate estimation. The slope of the line drawn between these two points appears closest to the opposite of the slope of the function at x=0.

Answer 1

2. B. The rate of change is 2

3. C. The rate of change is 2 inches per hour

4. B. The rate of change is 1.25 degrees Fahrenheit per day

5. (-0.5, 3) and (0.5, 3) would provide the most accurate estimation. The slope of the line drawn between these two points appears closest to the slope of the function at x = 0

Explanation:

2. Using the points (-1, -1) and the (1, 3) we have;

The rate of change = (Change in the y-values)/(Corresponding change in the x-values)

The rate of change = (3 - (-1))/(1 - (-1)) = 4/2 = 2

The rate of change is 2

3. Using the points (0, 0) and the (5, 10) we have;

The rate of change = (Change in the y-values)/(Corresponding change in the x-values)

Given that the function is a linear function, the rate of change of the function at 3 hours is given by the slope, m, as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

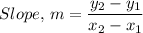
Where;

(x₁, y₁) = (0, 0)

(x₂, y₂) = (5, 10)

The y-coordinate being the inches of snow, and the x-coordinate being the time in hours, we have;

The rate of change = (10 - 0)/(5 - 0) = 10/5 = 2

The rate of change is 2 inches per hour

4. Given that the function is a linear function, the rate of change of the function at ninth day is given by the slope, m, as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

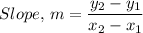
Where;

(x₁, y₁) = (2, 55)

(x₂, y₂) = (10, 65)

The y-coordinate being the temperature in degrees, and the x-coordinate being the time in days, we have;

`Slope, \, m =(65-55)/(10-2) = (10)/(8) = 1.25`

The rate of change is 1.25 degrees Fahrenheit per day

5. The points on the graph of the function that come before and after the point where the graph of the function crosses y-axis (the y-intercept) and are close to point are (-0.5, 2) and (0.5, 3)

Therefore, (-0.5, 2) and (0.5, 3) would provide the most accurate estimation. The slope of the line drawn between these two points appears closest to the slope of the function at x = 0.