Question

What is the integration of ∫e²ⁿdx please answer as fast as possible. ​

Answer 1

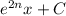`e^(2n)x + C` (since n is assumed to be a constant when integrating with respect to x)

Explanation:

You are integrating with respect to x, but
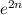`e^(2n)` has no x-terms. Thus, it is considered a constant. The integral of any constant is equal to the constant multiplied by x.

Example: the integral of 2 is 2x, since the derivative of 2x is 2.

`\int {e^(2n)} \, dx = e^(2n)x + C`

If you were integrating
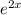`e^(2x)` with respect to x, it would look like this:

Since...

`(d)/(dx) (e^(ax)) = ae^(ax)`

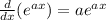
The integral of
`e^(ax)` is:

`\int{e^(ax)} \, dx = (e^(ax))/(a) + C`

`\int {e^(2x)} \, dx = (e^(2x))/(2) + C`

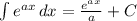
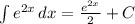
Note: C is a constant. It can be any number.

Answer:
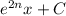`e^(2n)x + C` (since n is assumed to be a constant)