Answer :
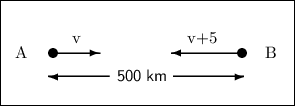
Distance between both buses = 500km
Time taken by them to meet each other = 4hr
Let speed of bus A be v km/hr.
ATQ, speed of bus B is 5km/ hr more than that of bus A.
∴ Speed of bus B will be (v + 5) km/hr.
★ Diagram :
★ As we know that,
- Speed = Distance/Time ... (I)
Assuming both buses as point masses,
Relative speed of object A wrt object B when the object B moves in the opposite direction of A is given by
Relative speed of bus A wrt B :
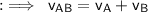

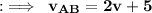
By substituting values in (I), we get
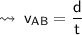
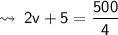
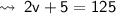
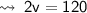

Speed of bus B = (v + 5)
Hope It Helps!