Answer:
a
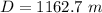
b
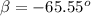
Step-by-step explanation:
From the question we are told that
The speed of the airplane is
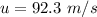
The angle is
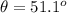
The altitude of the plane is
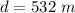
Generally the y-component of the airplanes velocity is
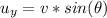
=>

=>
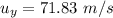
Generally the displacement traveled by the package in the vertical direction is
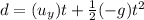
=>
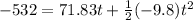
Here the negative sign for the distance show that the direction is along the negative y-axis
=>
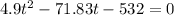
Solving this using quadratic formula we obtain that

Generally the x-component of the velocity is
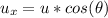
=>
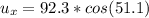
=>
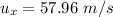
Generally the distance travel in the horizontal direction is
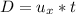
=>

=>
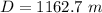
Generally the angle of the velocity vector relative to the ground is mathematically represented as
![\beta = tan ^(-1)[(v_y)/(v_x ) ]](https://img.qammunity.org/2021/formulas/physics/college/yel0yte7bab2tizxzb7f05ufx3s003bka9.png)
Here
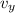 is the final velocity of the package along the vertical axis and this is mathematically represented as
is the final velocity of the package along the vertical axis and this is mathematically represented as
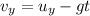
=>

=>
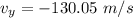
and v_x is the final velocity of the package which is equivalent to the initial velocity

So
![\beta = tan ^(-1)[-130.05}{57.96 } ]](https://img.qammunity.org/2021/formulas/physics/college/tbkz62l8bwju30tmk9oc48zh83gw0xl6nc.png)
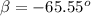
The negative direction show that it is moving towards the south east direction