Answer:
All answers EXCEPT answer C. are perfect square trinomials.
Explanation:
A perfect square trinomial is polynomial that satisfies the following condition:
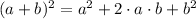 ,
,
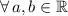
Let prove if each option observe this:
a)
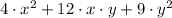
1)
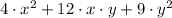 Given
Given
2)
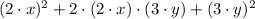 Definition of power/Distributive, associative and commutative properties.
Definition of power/Distributive, associative and commutative properties.
3)
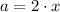 ,
,
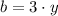 Definition of perfect square trinomial/Result.
Definition of perfect square trinomial/Result.
b)
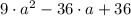
1)
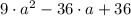 Given.
Given.
2)
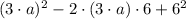 Definition of power/Distributive, associative and commutative properties.
Definition of power/Distributive, associative and commutative properties.
3)
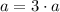 ,
,
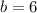 Definition of perfect square trinomial/Result.
Definition of perfect square trinomial/Result.
c)
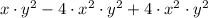
1)
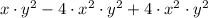 Given
Given
2)
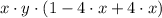 Distributive property.
Distributive property.
3)
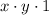 Existence of the additive inverse/Modulative property.
Existence of the additive inverse/Modulative property.
4)
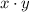 Modulative property/Result.
Modulative property/Result.
d)
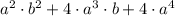
1)
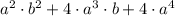 Given
Given
2)
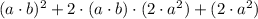 Definition of power/Distributive, associative and commutative properties.
Definition of power/Distributive, associative and commutative properties.
3)
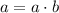 ,
,
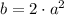 Definition of perfect square trinomial.
Definition of perfect square trinomial.
All answers EXCEPT answer C. are perfect square trinomials.