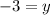Answer:

Explanation:
We have:
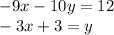
Since we already have a variable value (
 ) in the second equation, it would be easiest to substitute the value for
) in the second equation, it would be easiest to substitute the value for
 in the first equation:
in the first equation:

Distribute
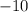 into
into
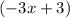 :
:

Combine like terms:
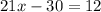
Add
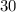 to both sides of the equation:
to both sides of the equation:

Divide by the coefficient of
 , which is
, which is
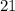 :
:

_
Now that we have our
 value, we can substitute that in to the second equation to find our
value, we can substitute that in to the second equation to find our
 value:
value:
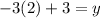
Multiply:
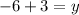
Combine like terms: