Answer:
sinФ = 8/17
cosФ = 15/17
tan Ф = 8/15
csc Ф = 17/8
sec Ф = 17/15
cot Ф = 15/8
Explanation:
Let us revise the trigonometry functions
- Sin(x) = opposite/hypotenuse
- Cos(x) = adjacent/hypoteouse
- Tan(x) = opposite/adjacent
- Csc(x) = hypotenuse/opposit
- Sec(x) = hypotenues/adjacent
- Cot(x) = adjacent/opposite
In the given figure
The opposite side to angle Ф = 8
The adjacent side to angle Ф = 15
Find the hypotenuse using Pythagoras' theorem
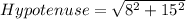
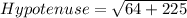
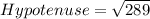
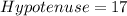
Let us use the rules above to find the trigonometry functions
sinФ = 8/17
cosФ = 15/17
tan Ф = 8/15
csc Ф = 17/8
sec Ф = 17/15
cot Ф = 15/8