Answer:
No values of x can make f(x)=6
Explanation:
Equation with Absolute Value
The absolute value of a number is always positive. That condition must be met when solving equations. Any condition that goes against the rule, must be discarded and not part of the solution.
The function provided in the question is:

We need to find the value(s) of x that make:
f(x)=6
It needs to solve the equation:
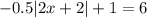
Subtracting 1:

Dividing by -0.5:

We reach to this equation to solve:

As stated above, the absolute value is always positive, and the equation forces the absolute value to be negative. There is no possible value of x that makes the absolute value negative, thus:
No values of x can make f(x)=6