Question

sixteen men working 9 hrs a day can complete a pice of work in 14 days .How many more men working 7 hrs a day would complete the same job in 12 days ?​

Answer 1

8 more men are needed to complete the job

Explanation:

Proportions

This problem can be solved by step-by-step reasoning applying proportions:

• 16 men working 9 hrs a day complete the job in 14 days
• 16 men working 1 hr a day complete the job in 14*9 days

The above statement stands because the fewer hours of work, the more time the job needs to be completed. Let's continue.

• 1 man working 1 hr a day complete the job in 14*9*16 days

The same reasoning applies here, fewer men=more days.

Now for the second condition. Increase the hours/day:

• 1 man working 7 hrs a day complete the job in 14*9*16/7 days

More hours/day=less days to complete the job

• x men working 7 hrs a day complete the job in 14*9*16/(7*x) days

We know this last time is 12 days, thus:

`\displaystyle 12=(14*9*16)/(7*x)`

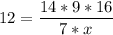
Solving for x:

`\displaystyle x=(14*9*16)/(7*12)=(2016)/(84)=24`

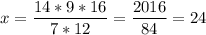
24 men are needed now, this is an increase of 24-16=8 more men

8 more men are needed to complete the job