Question

3 Given 7x + 2 > 58, which number is not in the solution set?

(1) 6
2: 8
(3) 10
(4) 12

Answer 1

`\rule{50}{1}\large\textsf{\textbf{\underline{Question:-}}}\rule{50}{1}`

Given 7x+2>58, which number is not in the solution set?

`\rule{50}{1}\large\blue\textsf{\textbf{\underline{Answer \& how to solve:-}}}\rule{50}{1}`

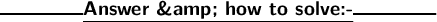
First, subtract 2 on both sides:-

`\sf{7x > 56}`

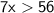
Now divide by 7 on both sides:-

`\sf{x > 8}`

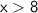
Henceforth, We conclude that

`\large\textsf{Numbers greater than 8 make this inequality true}`.

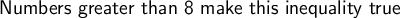Edit:- Option A (6) is the correct answer, since it's not greater than 8, so it doesn't satisfy the inequality.

Good luck with your studies.

`\rule{50}{1}\smile\smile\smile\smile\smile\rule{50}{1}`

Answer 2

(1) 6

Explanation:

Let's start by solving the inequality.

7x +2 > 58

Minus 2 on both sides:

7x > 58 -2

7x > 56

Divide both sides by 7:

x > 56 ÷7

x > 8

This means that the value of x has to be greater than 8. 6 is smaller than 8, and is therefore not in the solution set. Thus, option 1 is the correct answer.