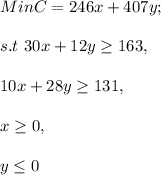Question

A certain academic department at a local university will conduct a research project. The department will need to hire graduate research assistants and professional researchers. Each graduate research assistant will need to work 30 hours per week on fieldwork and 10 hours per week at the university's research center. Each professional researcher will need to work 12 hours per week on fieldwork and 28 hours per week at the university's research center. The minimum number of hours needed per week for fieldwork is 163 and the minimum number of hours needed per week at the research center is 131. Each research assistant will be paid $246 per week and each professional researcher will be paid $407 per week. Let x denote the number of graduate research assistants hired and let y denote the number of professional researcher hired. The department wants to minimize cost. Set up the Linear Programming Problem for this situation.a) Min C = 246x + 407y; s.t 30x + 12y ≥ 163, 10x + 28y ≥ 131, x ≥ 0, y ≥ 0b) Min C = 246x + 407y; s.t 12x + 30y ≤ 131, 28x + 10y ≤ 163, x ≥ 0, y ≥ 0c) Min C = 246x + 407y; s.t 30x + 12y ≥ 163, 28x + 10y ≥ 131, x ≥ 0, y ≥ 0d) Min C = 407x + 246y; s.t 30x + 10y ≥ 163, 12x + 28y ≥ 131, x ≥ 0, y ≥ 0e) Min C = 407x + 246y; s.t 12x + 30y ≥ 163, 28x + 10y ≥ 131, x ≥ 0, y ≥ 0f) None of the above.

Answer 1

The answer is "Option a".

Explanation:

In the question, Option a is correct, because in this choice, Let x determine its amount of pupils hired and the point y is let as it's mean that it is the number of experts who recruited in the researcher, and description of the choice can be defined as follows:

`Min C = 246x + 407y; \\\\s.t \ 30 x + 12 y \geq 163, \\\\10x + 28y \geq 131, \\\\x \geq 0, \\\\y \leq 0\\\\`