Question

While traveling across flat land, you notice a mountain directly in front of you. The angle of elevation to the peak is 1.5°. After you drive 23 miles closer to the mountain, the angle of elevation is 13°. Approximate the height of the mountain.​

Answer 1

0.68 miles

Explanation:

Let's say that the height of the mountain is h

The distance between the mountain and the car, after moving 23 miles closer to the mountain, will be x (let's pose it as x for now)

tan(1.5°) = opposite/adjacent = h/23 + a

=> h = (23 + a)tan(1.5°) ---- (1)

tan(13°) = h/a

=> h = a(tan(13°)) ---- (2)

Now since h is common among the two equations, we can equate them;

`\left(23+a\right)\tan \left(1.5^(\circ \:)\right)=a\left(\tan \left(13^(\circ \:)\right)\right),\\23\tan \left(1.5^(\circ \:)\right)+\tan \left(1.5^(\circ \:)\right)a=\tan \left(13^(\circ \:)\right)a,\\\\\tan \left(1.5^(\circ \:)\right)a-\tan \left(13^(\circ \:)\right)a=-23\tan \left(1.5^(\circ \:)\right),\\\left(\tan \left(1.5^(\circ \:)\right)-\tan \left(13^(\circ \:)\right)\right)a=-23\tan \left(1.5^(\circ \:)\right),\\\\`

`a=(23\tan \left(1.5^(\circ \:)\right))/(\tan \left(13^(\circ \:)\right)-\tan \left(1.5^(\circ \:)\right)) = 2.94249...`

`h = 2.94249tan\left(13^(\circ )\right) = 0.67932\dots`

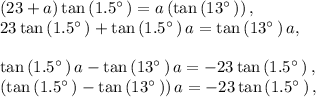
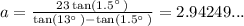
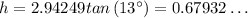
The height of the mountain ≈ 0.68 miles