
Given 7x+2>58, which number is not in the solution set?
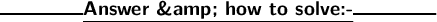
First, subtract 2 on both sides:-
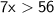
Now divide by 7 on both sides:-
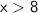
Henceforth, We conclude that
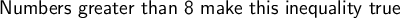 .
.
Edit:- Option A (6) is the correct answer, since it's not greater than 8, so it doesn't satisfy the inequality.
Good luck with your studies.
