Answer:
(a) As time increases, the amount of water in the pool increases.
11 gallons per minute
(b) 65 gallons
Explanation:
From inspection of the table, we can see that as time increases, the amount of water in the pool increases.
We are told that Ann adds water at a constant rate. Therefore, this can be modeled as a linear function.
The rate at which the water is increasing is the rate of change (which is also the slope of a linear function).
Choose 2 ordered pairs from the table:

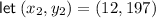
Input these into the slope formula:
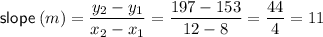
Therefore, the rate at which the water in the pool is increasing is:
11 gallons per minute
To find the amount of water that was already in the pool when Ann started adding water, we need to create a linear equation using the found slope and one of the ordered pairs with the point-slope formula:

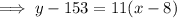
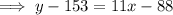
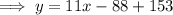
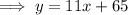
When Ann had added no water, x = 0. Therefore,
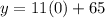
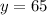
So there was 65 gallons of water in the pool before Ann starting adding water.