Question

QUADRATIC FORMULA

11. The current World Record for the Track event Shot Put is 23.37 meters - meaning the Shot landed
23.37 meters from where it was launched (DO NOT USE THIS VALUE FOR THE EQUATION).
The path of the Shot thrown by an athlete during a track meet can be modeled by the Quadratic Equation
h(t) = -0.09c2 + 2t + 1.67 where he represents its height in meters and m represents the horizontal
distance in meters. How far did the Shot land from where it was thrown? Substitute 0 for h in your Equation
in order to find the horizontal distance from where this Shot was lauchedlaunched.

Answer 1

23.028 meters

Explanation:

We presume your quadratic equation is intended to be ...

h(m) = -0.09m² +2m +1.67

where h(m) is the height in meters, and m is the horizontal distance in meters. You want to find the positive value of m when h = 0.

__

The quadratic formula tells you the solution to ...

ax² +bx +c = 0

In your equation, a = -0.09, b = 2, c = 1.67, and the variable is m. The solutions given by the formula are ...

`m=(-b\pm√(b^2-4ac))/(2a)=(-2\pm√(2^2-4(-0.09)(1.67)))/(2(-0.09))\\\\=(2\pm√(4+0.6012))/(0.18)\approx\{-0.806,23.028\}`

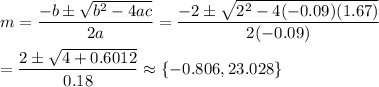
The shot landed about 23.028 meters from where it was thrown.

_____

Additional comment

The shot was launched at an angle of about 63.4° from the horizontal. Had a shallower angle been used with the same launch speed (about 16.5 m/s), the shot would have traveled farther. At about 45°, the distance might have been in excess of 29 meters.