Question

Vectors A and B lie in the xy ‑plane. Vector A has a magnitude of 17.1 and is at an angle of 150.5∘ counterclockwise from the +x ‑axis. Vector B has a magnitude of 28.1 and is 205.3∘ from the +x ‑axis. Resolve A and B into components, and express using ???????????? unit vectors,

A =Ax????+Ay????+Az????
B =Bx????+By????+Bz????
where Ax, Ay, Az and Bx, By, and Bz are the calculated values of the x ‑, y ‑, and z ‑components of vectors A and B , respectively.

Answer 1

A = -14.87 i ^ + 8.42 j ^ + 0 k ^

B = -25.41 i ^ -12.0 j ^ + 0 k ^

Step-by-step explanation:

For this exercise let's use trigonometry by decomposing to vectors

vector A

module 17.1 with an angle of 150.5 counterclockwise.

Sin 150.5 =
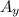`A_(y)` / A

cos 150.5 = Ax / A

A_{y} = A sin 150.5 = 17.1 sin 150.5

Aₓ = A cos 1505 = 172 cos 150.5

A_{y} = 8,420

Aₓ = -14.870

the vector is

A = -14.87 i ^ + 8.42 j ^ + 0 k ^

Vector B

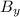`B_(y)` = 28.1 sin 205.3

Bₓ = 28.1 cos 205.3

B_{y} = -12.009

Bₓ = -25.405

the vector is

B = -25.41 i ^ -12.0 j ^ + 0 k ^