Question

Mr. Ratchett, an elderly American, was found murdered in his train compartment on the Orient Express at 7 AM. When his body was discovered, the famous detective Hercule Poirot noted that Ratchett had a body temperature of 28 degrees. The body had cooled to a temperature of 27 degrees one hour later. If the normal temperature of a human being is 37 degrees and the air temperature in the train is 22 degrees.

Required:
Estimate the time of Ratchett's death using Newton's Law of Cooling.

Answer 1

To estimate the time of Ratchett's death using Newton's Law of Cooling, we can use the equation T(t) = T1 + (T2 - T1) * e(-kt). By plugging in the given values, we can solve for time and estimate the time of death to be approximately 46.75 minutes.

Step-by-step explanation:

To estimate the time of Ratchett's death using Newton's Law of Cooling, we can use the equation:

T(t) = T₁ + (T₂ - T₁) * e-kt

where T(t) is the temperature at time t, T₁ is the initial temperature, T₂ is the air temperature, k is the constant, and e is the base of the natural logarithm.

Using the given information, we can plug in the values and solve for time:

27 = 28 + (22 - 28) * e-k

e-k = -1/6

-k = ln(-1/6)

k = -ln(1/6)

Now we can plug in the values and solve for time:

37 = 28 + (22 - 28) * e-ln(1/6)t

e-ln(1/6)t = 9/6

t = -ln(9/6)/ln(1/6)

Using a calculator, we find that t is approximately 0.779 hours, or 46.75 minutes.

Answer 2

Answer: Mr. Ratchett died approximately at 2AM.

Step-by-step explanation: Newton's Law of Cooling shows the cooling rate between a body and the environment, by stating that the rate is proportional to the difference in temperatures between them.

Mathematically, it is represented as:

`(dQ)/(dt)=\alpha.A.(T_(s)-T)`

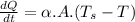
This differential equation solved, gives the solution:

`T(t)=T_(s)+(T_(0)-T_(s))e^(-kt)`

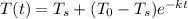
where

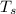`T_(s)` is temperature of the environment

`T_(0)` is the initial temperature of the body

k is a parameter dependent of heat transfer coefficient, heat capacity and area of the body

t is time required to change the temperature

For the murder on the Orient Express, first determine parameter k.

In 1 hour, Mr. Ratchett's body decrease 1°:

`27=22+(28-22)e^(-1k)`

`5=6e^(-k)`

`e^(-k)=(5)/(6)`

`ln(e^(-k))=ln(0.834)`

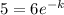
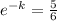
k = 0.1823

Using the parameter, find estimate time:

`28=22+(37-22)e^(-0.1823t)`

`6=15e^(-0.1823t)`

`ln(e^(-0.1823t))=ln(0.4)`

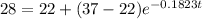
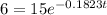
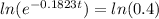
0.1823t = 0.9163

`t=(0.9163)/(0.1823)`

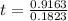
t ≈ 5 hours

The body was found at 7AM. So, it took approximately 5 hours to cool down to 28° at that time. Therefore, Mr. Ratchett died at 2AM.