Question

The probability density function of the time to failure of an electronic component in a copier (in hours) is f(x) for Determine the probability that

a. A component lasts more than 3000 hours before failure.
b. A component fails in the interval from 1000 to 2000 hours.
c. A component fails before 1000 hours.
d. Determine the number of hours at which 10% of all components have failed.

Answer 1

The question is incomplete. Here is the complete question.

The probability density function of the time to failure of an electronic component in a copier (in hours) is

`f(x)=\frac{e^{(-x)/(1000) }}{1000}`

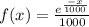
for x > 0. Determine the probability that

a. A component lasts more than 3000 hours before failure.

b. A componenet fails in the interval from 1000 to 2000 hours.

c. A component fails before 1000 hours.

d. Determine the number of hours at which 10% of all components have failed.

Answer: a. P(x>3000) = 0.5

b. P(1000<x<2000) = 0.2325

c. P(x<1000) = 0.6321

d. 105.4 hours

Explanation: Probability Density Function is a function defining the probability of an outcome for a discrete random variable and is mathematically defined as the derivative of the distribution function.

So, probability function is given by:

P(a<x<b) =
`\int\limits^b_a {P(x)} \, dx`

Then, for the electronic component, probability will be:

P(a<x<b) =
`\int\limits^b_a {\frac{e^{(-x)/(1000) }}{1000} } \, dx`

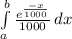
P(a<x<b) =
`(1000)/(1000).e^{(-x)/(1000) }`

P(a<x<b) =
`e^{(-b)/(1000) }-e^(-a)/(1000)`

a. For a component to last more than 3000 hours:

P(3000<x<∞) =
`e^{(-3000)/(1000) }-e^(-a)/(1000)`

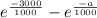
Exponential equation to the infinity tends to zero, so:

P(3000<x<∞) =
`e^(-3)`

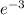
P(3000<x<∞) = 0.05

There is a probability of 5% of a component to last more than 3000 hours.

b. Probability between 1000 and 2000 hours:

P(1000<x<2000) =
`e^{(-2000)/(1000) }-e^(-1000)/(1000)`

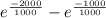
P(1000<x<2000) =
`e^(-2)-e^(-1)`

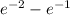
P(1000<x<2000) = 0.2325

There is a probability of 23.25% of failure in that interval.

c. Probability of failing between 0 and 1000 hours:

P(0<x<1000) =
`e^{(-1000)/(1000) }-e^(-0)/(1000)`

P(0<x<1000) =
`e^(-1)-1`

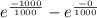
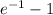
P(0<x<1000) = 0.6321

There is a probability of 63.21% of failing before 1000 hours.

d. P(x) =
`e^{(-b)/(1000) }-e^(-a)/(1000)`

0.1 =
`1-e^(-x)/(1000)`

`-e^{(-x)/(1000) }=-0.9`

`{(-x)/(1000) }=ln0.9`

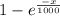
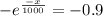
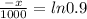
-x = -1000.ln(0.9)

x = 105.4

10% of the components will have failed at 105.4 hours.