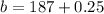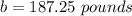Answer:
First Question
lower limit of 9 mph

upper limit of 9 mph
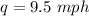
Second Question
lower limit of 120 pounds is
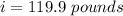
upper limit of 120 pounds is
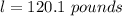
Third Question
lower limit of 187 pounds is
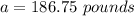
upper limit of 187 pounds is
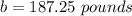
Explanation:
From the question we are told that
The amount of beer administered is three 12-ounce beers
The amount of coffee administered is two cups of coffee
The speed limit is 60-mph
The smallest unit of scale is 1 mph
The first subject scores 9 mph
Generally given that the smallest unit of scale is 1 mph then the deviation of 9 mph will be by
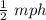
Hence the lower limit of 9 mph is


And the upper limit of 9 mph is
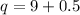
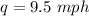
Generally given that the measuring weight on a scale that is accurate to the nearest 0.2 pound then 120 pounds will deviate by

Hence the lower limit of 120 pounds is
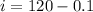
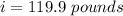
And the upper limit of 120 pounds is
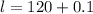
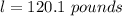
Generally given that the measuring weight on a scale that is accurate to the nearest 0.5 pound then 187 pounds will deviate by
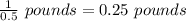
Hence the lower limit of 120 pounds is
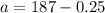
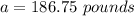
And the upper limit of 120 pounds is