Question

Maria and John decide to shop for furnishings for the new house. They choose items that amount to $5600.00. The store has 2 fixed installment simple interest loan options for purchasing:

Option 1: 20% down payment and financing at 5% simple interest per year for 3 years.

Option 2: no down payment and financing at 5.25% simple interest for 4 years.

Answer each of the following questions separately, showing all your work to reach each answer.

A. Which option will result in smaller finance charge (interest)? What will that finance charge/interest be?

B. Which option will result in the smaller monthly payment on this fixed installment loan? What will that monthly payment be?

C. They decide to defer any purchases and invest a $5600 bonus that Maria will be getting from work in a savings account. The APR is 21.6% compounded monthly. How much interest will they earn in 4 years?

D. They decide to defer any purchases and loan the $5600 bonus to a needy relative at 1.5% simple interest per year. How long will the term of the loan need to be if they want to earn $500 in interest (assuming the loan is not paid off early).

Answer 1

A. The option that results in the smaller finance charge/interest is option 1

B. The option that will result in the smaller monthly payment is option 1

C. The interest they will earn in 4 years, I = $6,643.972

D. The time it will take for them to earn an interest of $500 by loaning $5,600 at 1.5% is approximately 5.95 years

Explanation:

A. The simple interest, I, formula is given as follows;

`I = (P * R * T )/(100)`

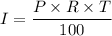
Where;

P = The principal

R = The rate

T =The time given for the loan

For Option 1 the first option, we have;

Down payment = 0.2 × $5600.00 = $1,120.00

Principal = $5600.00 - $1,120.00 = $4,480.00

`\therefore I = (\$ 4480* 5 * 3 )/(100) = \$672`

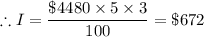
For Option 2. the second option, we have;

P = $5600.00

`\therefore I = (\$ 5600 * 5.25 * 3 )/(100) = \$1176`

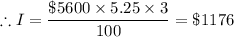
The option that results in the smaller finance charge is option 1

B. For option 1, the total amount = Principal + Interest

∴ The total amount remaining = $4480 + $672 = $5,152

The monthly payment = A/N

Where;

A = The total amount yet to be paid out of the loan = $5,152

N = The number of time periods = 3 × 12 = 36 months

The monthly payment = $5,152/36 =
`\$ 143.\overline{111}`

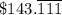
For option 2, the total amount = Principal + Interest

∴ The total amount remaining = $5,600 + $1176 = $6776

The monthly payment = A/N

Where;

A = The total amount yet to be paid out of the loan = $6,776

N = The number of time periods = 3 × 12 = 36 months

The monthly payment = $6,776/36 =
`\$ 188.\overline{222}`

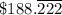
Therefore, the option that will result in the smaller monthly payment is option 1

C. For a compound interest on a principal of $5,600 invested for 4 years in a savings account that gives an interest rate 21.6% per annum, we have;

`A = P * \left(1 + (r)/(n) \right)^((n* t))`

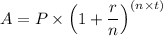
We have, using the annual rate, rather than calculating for the monthly rate;

`A = 5600 * \left(1 + 0.216 \right)^(4) \approx 12243.972`

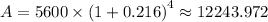
Therefore, the amount they will have in 4 years ≈ $ 12,243.972

The interest they will earn in 4 years, I = A - P ≈ $ 12,243.972 - $5,600 = $6,643.972

The interest they will earn in 4 years, I = $6,643.972

D. To earn an interest of $500 at an interest rate of 1.5%, we have;

`500 = (5600 * 1.5 * T)/(100) = 84 * T`

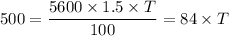
From which we have;

`T = (500)/(84) = (125)/(21) = 5(20)/(21) \approx 5.95`

Therefore, the time it will take for them to earn an interest of $500 by loaning $5,600 at 1.5% is approximately 5.95 years.