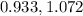Answer:
a

b
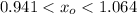
c
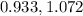
Explanation:
From the question we are told that
The data is
1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 1.01, 1.03, 0.99, 1.00, 1.00, 0.99, 0.98, 1.01, 1.02, 0.99
Generally sample mean is mathematically represented as
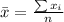
=>
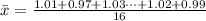
=>
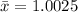
Generally the standard deviation is mathematically represented as
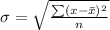
=>
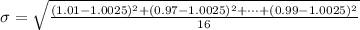
=>
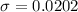
Given that the confidence level is 99% then the level of significance is
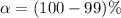
=>

From the t distribution table the critical value for
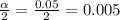 is
is

Generally the margin of error is mathematically represented as
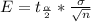
=>
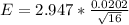
=>
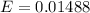
Generally the 99% confidence interval is
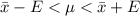
=>
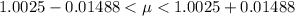
=>

Generally the 99% Prediction interval is mathematically represented as
![\= x -[t_{(\alpha )/(2) } * \sigma * \sqrt{1 + (1)/(n) } ] < x_o <\= x +[t_{(\alpha )/(2) } * \sigma * \sqrt{1 + (1)/(n) } ]](https://img.qammunity.org/2021/formulas/mathematics/college/e6bfbhctn7gvn1z0vrdg0o8x4ixjehj0vx.png)
So
=>
![1.0025 -[2.947 * 0.0202 * \sqrt{1 + (1)/(16) } ] < x_o <1.0025 +[2.947 * 0.0202 * \sqrt{1 + (1)/(16) } ] </p><p>=> [tex]0.941 < x_o < 1.064](https://img.qammunity.org/2021/formulas/mathematics/college/hkzdvr1u1xr9vic13vit5u7kmcu725uzl1.png)
Generally the two sided limit tolerance factor at sample size of n = 16 , Prediction level of 99% and confidence level of 95 is
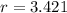 , this value is obtained from the statistical table
, this value is obtained from the statistical table
Generally the 99% tolerance interval for coverage of the central 95% of the distribution of diameters is mathematically represented as
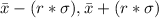
=>
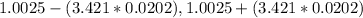
=>