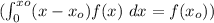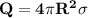Answer:
Step-by-step explanation:
From the given information:
We know that the thin spherical shell is on a uniform surface which implies that both the inside and outside the charge of the sphere are equal, Then
The volume charge distribution relates to the radial direction at r = R
∴
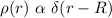
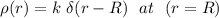
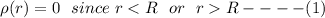
To find the constant k, we examine the total charge Q which is:
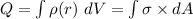
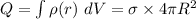
∴
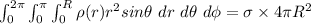
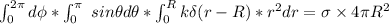
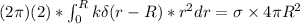
Thus;
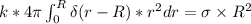
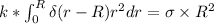
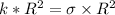

Hence, from equation (1), if k =
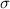
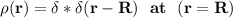
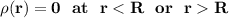
To verify the units:

↓ ↓ ↓
c/m³ c/m³ × 1/m
Thus, the units are verified.
The integrated charge Q
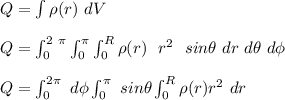
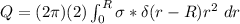
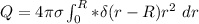
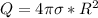 since
since