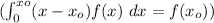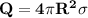Question

A thin spherical spherical shell of radius R which carried a uniform surface charge density σ. Write an expression for the volume charge density rho(r) of this thin shell distribution in terms of σ and an appropriate delta function. Verify explicitly that the units of your final expression are correct. Also show that your total integrated charge comes out right.

Answer 1

Step-by-step explanation:

From the given information:

We know that the thin spherical shell is on a uniform surface which implies that both the inside and outside the charge of the sphere are equal, Then

The volume charge distribution relates to the radial direction at r = R

∴

`\rho (r) \ \alpha \ \delta (r -R)`

`\rho (r) = k \ \delta (r -R) \ \ at \ \ (r = R)`

`\rho (r) = 0\ \ since \ r< R \ \ or \ \ r>R---- (1)`

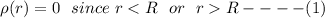
To find the constant k, we examine the total charge Q which is:

`Q = \int \rho (r) \ dV = \int \sigma * dA`

`Q = \int \rho (r) \ dV = \sigma *4 \pi R^2`

∴

`\int ^(2 \pi)_(0) \int ^(\pi)_(0) \int ^(R)_(0) \rho (r) r^2sin \theta \ dr \ d\theta \ d\phi = \sigma * 4 \pi R^2`

`\int^(2 \pi)_(0) d \phi* \int ^(\pi)_(0) \ sin \theta d \theta * \int ^(R)_(0) k \delta (r -R) * r^2dr = \sigma * 4 \pi R^2`

`(2 \pi)(2) * \int ^(R)_(0) k \delta (r -R) * r^2dr = \sigma * 4 \pi R^2`

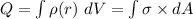
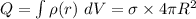
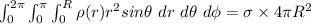
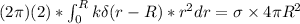
Thus;

`k * 4 \pi \int ^(R)_(0) \delta (r -R) * r^2dr = \sigma * R^2`

`k * \int ^(R)_(0) \delta (r -R) r^2dr = \sigma * R^2`

`k * R^2= \sigma * R^2`

`k = R^2 --- (2)`

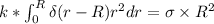
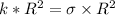
Hence, from equation (1), if k =
`\sigma`

`\mathbf{\rho (r) = \delta* \delta (r -R) \ \ at \ \ (r=R)}`

`\mathbf{\rho (r) =0 \ \ at \ \ r<R \ \ or \ \ r>R}`

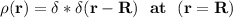
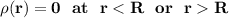
To verify the units:

`\mathbf{\rho (r) =\sigma \ * \ \delta (r-R)}`

↓ ↓ ↓

c/m³ c/m³ × 1/m

Thus, the units are verified.

The integrated charge Q

`Q = \int \rho (r) \ dV \\ \\ Q = \int ^(2 \ \pi)_(0) \int ^(\pi)_(0) \int ^R_0 \rho (r) \ \ r^2 \ \ sin \theta \ dr \ d\theta \ d \phi \\ \\ Q = \int ^(2 \pi)_(0) \ d \phi \int ^(\pi)_(0) \ sin \theta \int ^R_(0) \rho (r) r^2 \ dr`

`Q = (2 \pi) (2) \int ^R_0 \sigma * \delta (r-R) r^2 \ dr`

`Q = 4 \pi \sigma \int ^R_0 * \delta (r-R) r^2 \ dr`

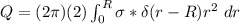
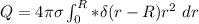
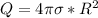`Q = 4 \pi \sigma *R^2` since
`( \int ^(xo)_(0) (x -x_o) f(x) \ dx = f(x_o) )`

`\mathbf{Q = 4 \pi R^2 \sigma }`