Question

Juan's class is going to construct an outdoor garden. The garden will be in the shape of a square, Juan's teacher gave the class three

options for the area of the garden: 30 square feet, 40 square feet, or 50 square feet.
Part A
Without using a calculator, approximate the side length, to the nearest tenth of a foot, for the garden with an area of 30 square fet. Show
your work.
Part B
The other two garden options have approximate side lengths of 6.3 feet and 7.1 feet. Locate and graph the three points on a horizontal
number line to show the approximation of the side length for each option.

Answer 1

Part A: 5.5

Part B: Kindly refer to the attached image for the number line representation.

Explanation:

Given that:

Possible area of the first garden = 30 sq ft

Possible area of the second garden = 40 sq ft

Possible length of the second garden = 6.3 ft

Possible area of the third garden = 50 sq ft

Possible length of the third garden = 7.1 ft

To find:

Part A: Side length of the square with area 30 sq ft to the nearest tenth.

Part B: Locating and graphing the three points on a horizontal number line.

Solution:

Formula for area of a square:

`Area =(Side)^2`

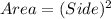
Part A: Given that area = 30 sq ft

Putting in the formula to find the value:

`30=Side^2\\\Rightarrow Side = 5.477 \approx \bold{5.5\ ft}`

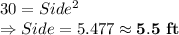
Part B:

Kindly refer to the attached image for the number line representation of the given two lengths and the length calculated for the first square.

The three lengths are 5.5, 6.3 and 7.1 respectively.

The three numbers to located on the graph are = 5.5, 6.3 and 7.1