Question

Holly is taking out a loan in the amount of $10,000. Her choices for the loan are a 4-year loan at 4% simple interest and a 6-year loan at 5% simple interest. What is the difference in the amount of interest Holly would have to pay for each of these two loans?

Answer 1

1400

Explanation:

I got this question right...

Answer 2

The difference in the amount of interest she would have to pay for the two loans is $1,400

Explanation:

The amount of loan Holly is taking out, P = $10,000

The choices available for the loan are;

1) Loan duration, T₁ = 4-year

Interest rate, R₁ = 4%

2) Loan duration, T₂ = 6-year

Interest rate, R₂ = 5%

For the first choice, we have;

The simple interest, I, given by the formula;

`I_1 = (P * R_1 * T_1 )/(100) = (10,000 * 4 * 4 )/(100) = \$ 1,600`

For the second choice, we have;

The simple interest, I, given by the formula;

`I_2 = (P * R_2 * T_2 )/(100) = (10,000 * 5 * 6 )/(100) = \$ 3,000`

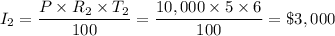
The difference, D, in the amount of interest she would have to pay for the two loans is therefore;

D = I₂ - I₁ = $3,000 - $1,600 = $1,400

The difference in the amount of interest she would have to pay for the two loans = D = $1,400.