Answer/Step-by-step explanation:
Given that P varies directly with r, the equation for this direct variation would be:
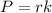 ,
,
Where,
P = power
r = radius
k = constant of variation.
If P = 550, when r = 11, constant of this direct variation is calculated as follows:
Plug in the values of P and r into the variation equation to find k.
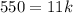
Divide both sides by 11
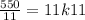
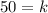
Constant of variation = 50
To find the radius (r) of the gear whose power (P) = 715, substitute P = 715 and k = 50 in the variation equation.
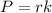
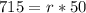
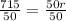
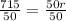
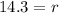
r = 14.3