Answer:
(a) The assumption regarding the distribution of the price of small computers which is necessary to test the analyst’s claim are;
- The data given must follow a normal distribution.
- The sample values are taken from the population data only.
(b) H0: μ ≥ 350; HA: μ < 350
(c) The value of the t-test statistic is -0.263.
(d) At a 5% significance level, the t table gives a critical value of -2.015 at 5 degrees of freedom for the left tailed test.
Explanation:
We are given that an analyst comments that the larger companies have a cause for concern since the mean price of these small computers has fallen below $350.
She examines six popular brands of these small computers and records their retail prices as given below:
$322, $269, $373, $412, $299, $389.
(a) The assumption regarding the distribution of the price of small computers which is necessary to test the analyst’s claim are;
- The data given must follow a normal distribution.
- The sample values are taken from the population data only.
(b) Let
 = population mean price of these small computers
= population mean price of these small computers
So, Null Hypothesis,
 : μ ≥ 350 {means that the mean price of these small computers is more than or equal to $350}
: μ ≥ 350 {means that the mean price of these small computers is more than or equal to $350}
Alternate Hypothesis,
 : μ < 350 {means that the mean price of these small computers has fallen below $350}
: μ < 350 {means that the mean price of these small computers has fallen below $350}
(c) The test statistics that will be used here is one-sample t-test statistics because we don't know about the population standard deviation;
T.S. =
 ~
~

where,
 = sample mean price =
= sample mean price =
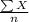 = $344
= $344
s = sample standard deviation =
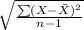 = $55.89
= $55.89
n = sample of prices = 6
So, the test statistics =
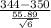 ~
~
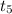
= -0.263
The value of the t-test statistic is -0.263.
(d) Now, at a 5% significance level, the t table gives a critical value of -2.015 at 5 degrees of freedom for the left tailed test.
Since the value of our test statistics is more than the critical value of t as -0.263 > -2.015, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.
Therefore, we conclude that the mean price of these small computers is more than or equal to $350.