Answer:
(i) The equivalent coordinates in rectangular form are
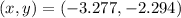 .
.
(ii) The equivalent coordinates in rectangular form are
 .
.
Explanation:
In this exercise we must find the equivalent coordinates in rectangular form from polar form. That is:
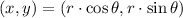
Where:
 - Norm of vector, dimensionless.
- Norm of vector, dimensionless.
 - Direction of vector with respect to +x semiaxis, measured in sexagesimal degrees.
- Direction of vector with respect to +x semiaxis, measured in sexagesimal degrees.
(i) (
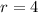 ,
,
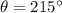 )
)
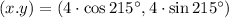
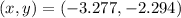
The equivalent coordinates in rectangular form are
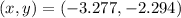 .
.
(ii) (
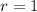 ,
,
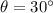 )
)
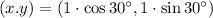

The equivalent coordinates in rectangular form are
 .
.