Question

Three potential employees took an aptitude test. Each person took a different version of the test. The scores are reported below. Tobias got a score of 74.7; this version has a mean of 61.7 and a standard deviation of 13. Norma got a score of 351; this version has a mean of 291 and a standard deviation of 25. Vincent got a score of 7.38; this version has a mean of 6.9 and a standard deviation of 0.4. If the company has only one position to fill and prefers to fill it with the applicant who performed best on the aptitude test, which of the applicants should be offered the job?

Answer 1

Norma performed best on the aptitude test and should be offered the job.

Explanation:

We are given that three potential employees took an aptitude test. Each person took a different version of the test. The scores are reported below. Tobias got a score of 74.7; this version has a mean of 61.7 and a standard deviation of 13. Norma got a score of 351; this version has a mean of 291 and a standard deviation of 25. Vincent got a score of 7.38; this version has a mean of 6.9 and a standard deviation of 0.4.

Now, to find which of the applicants should be offered the job, we have to find the z-score of each of the applicants, and the one who gets the highest z-score will get the job.

The z-score probability distribution for the normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean and
`\sigma` = standard deviation

Firstly, we will find the z-score for Tobias;

The z-score of 74.7 =
`(X-\mu)/(\sigma)`

=
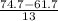`(74.7-61.7)/(13)` = 1

Now, we will find the z-score for Norma;

The z-score of 351 =
`(X-\mu)/(\sigma)`

=
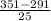`(351-291)/(25)` = 2.4

Now, we will find the z-score for Vincent;

The z-score of 7.38 =
`(X-\mu)/(\sigma)`

=
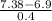`(7.38-6.9)/(0.4)` = 1.2

As we can clearly see that the z-score is highest for Norma which means that Norma performed best on the aptitude test and should be offered the job.