Question

Minnesota had the highest turnout rate of any state for the 2012 Presidential election (United States Election Project website, February 9, 2013). Political analysts wonder if turnout in rural Minnesota was higher than turnout in the urban areas of the state. A sample shows that 663 of 884 registered voters from rural Minnesota voted in the 2012 Presidential election, while 414 out of 575 registered voters from urban Minnesota voted.A. Formulate the null and alternative hypotheses that can be used to test whether registered voters in rural Minnesota were more likely than registered voters in urban Minnesota to vote in the 2012 Presidential election.1. H0: prural purban2. Ha: prural purbanB. What is the proportion of sampled registered voters in rural Minnesota that voted in the 2012 Presidential election?C. What is the proportion of sampled registered voters in urban Minnesota that voted in the 2012 Presidential election?D. At = .05, test the hypothesis. What is the p-value, and what conclusion do you to draw from your results?

Answer 1

Explained below.

Explanation:

In this case we need to determine whether registered voters in rural Minnesota were more likely than registered voters in urban Minnesota to vote in the 2012 Presidential election.

(A)

The hypothesis can be defined as follows:

H₀: The registered voters in rural Minnesota were not more likely than registered voters in urban Minnesota to vote in the 2012 Presidential election, i.e.
`p_(rural) - p_(urban)\leq 0`.

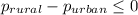Hₐ: The registered voters in rural Minnesota were more likely than registered voters in urban Minnesota to vote in the 2012 Presidential election, i.e.
`p_(rural) - p_(urban)> 0`.

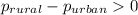(B)

Compute the proportion of sampled registered voters in rural Minnesota that voted in the 2012 Presidential election as follows:

`\hat p_(rural)=(663)/(884)=0.75`

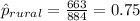
(C)

Compute the proportion of sampled registered voters in urban Minnesota that voted in the 2012 Presidential election as follows:

`\hat p_(urban)=(414)/(575)=0.72`

(D)

Compute the total proportion as follows:

`\hat p=(663+474)/(884+575)=0.74`

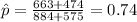
Compute the test statistic value as follows:

`Z=\frac{\hat p_(1)-\hat p_(2)}{\sqrt{\hat p(1-\hat p)* [(1)/(n_(1))+(1)/(n_(2))]}}`

`=\frac{0.75-0.72}{\sqrt{0.74(1-0.74)* [(1)/(884)+(1)/(575)]}}\\\\=1.28`

The test statistic value is 1.28.

The decision rule is:

The null hypothesis will be rejected if the p-value of the test is less than the significance level.

Compute the p-value as follows:

`p-value=P(Z>1.28)=1-P(Z<1.28)=1-0.89973=0.10027`

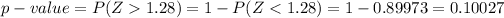
The p-value of the test is quite large. The null hypothesis will be rejected at 0.05 significance level.

Thus, there enough evidence suggesting that the registered voters in rural Minnesota were more likely than registered voters in urban Minnesota to vote in the 2012 Presidential election.