Question

Mimi sells super-sized cookies for $1.50 each and estimates she has expenses of $10 to make one batch of cookies. If the inequality 1.5x - 10 > y models this situation, how many cookies, x, would she need to sell to make a profit of at least $30? a: x > 20 cookies b: x > 26 cookies c: x > 27 cookies d: x > 35 cookies

Answer 1

(b) x > 26 cookies

Explanation:

The selling price of 1 super-sized cookie, S.P.=$1.50

Let a batch have x cookies.

So, the selling price of x cookies=1.5x

The expences in making one batch of cookies=$10

So, net profit = 1.5x-10

The given inequality to model this is 1.5x - 10 > y, That means the profit for one batch is greater than y.

As she wants to make a profit of at least $30, so for this condition, the value of y is 30.

Now, the given inequality become,

`1.5x - 10 >30`

`\Rightarrow 1.5x>30+10`

`\Rightarrow x>(40)/(1.5)`

`\Rightarrow x>26(2)/(3)`

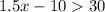
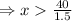
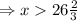
As x is the number of cookies, so, it can't have a fractional value. This can be written as

`x>26` or
`x\geq27.`

So, she has to sell more than 26 cookies to make a profit of at least $30.

Hence, option (b) is correct.