Given:
Demand equation :
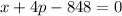 .
.
Supply equation :
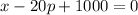
To find:
The equilibrium quantity and the equilibrium price for the GPS Navigators.
Solution:
Demand equation is
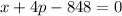
where x is the quantity demanded per week and p is the wholesale unit price in dollars.
Quantity demanded
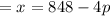 ...(i)
...(i)
Supply equation is
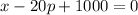
where x is the quantity the supplier will make available in the market each week when the wholesale price is p dollars each.
Quantity supplied
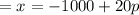 ...(ii)
...(ii)
For equilibrium, Quantity demanded = Quantity supplied.
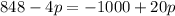


Divide both sides by p.
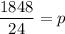
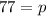
Substitute p=77 in (i), to find the equilibrium quantity.
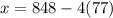
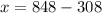
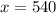
Therefore, the equilibrium quantity is 540 units per week and the equilibrium price is $77 for the GPS Navigators.