Answer:
a) True. The differential equation is
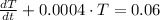 , where
, where
 is measured in Celsius.
is measured in Celsius.
b) The temperature of the object after 200 second inside the microwave is approximately 34.611 ºC.
Explanation:
a) The object is heated up by convection and radiation, from First Law of Thermodynamics we get that energy interactions on the object are represented by:
 (Eq. 1)
(Eq. 1)
Where:
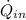 - Heat transfer rate to the object, measured in watts.
- Heat transfer rate to the object, measured in watts.
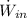 - Electric power given by the microwave owen, measured in watts.
- Electric power given by the microwave owen, measured in watts.
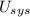 - Internal energy of the object, measured in watts.
- Internal energy of the object, measured in watts.
Then, we expand the expression by means of definition from Heat Transfer and Thermodynamics:
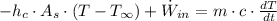
Where:
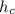 - Heat transfer coefficient, measured in watts per square meter-Celsius.
- Heat transfer coefficient, measured in watts per square meter-Celsius.
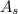 - Surface area of the object, measured in square meters.
- Surface area of the object, measured in square meters.
 - Temperature of the object, measured in Celsius.
- Temperature of the object, measured in Celsius.
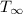 - Internal temperature of the microwave oven, measured in Celsius.
- Internal temperature of the microwave oven, measured in Celsius.
 - Mass of the object, measured in kilograms.
- Mass of the object, measured in kilograms.
 - Specific heat of the object, measured in joules per kilogram-Celsius.
- Specific heat of the object, measured in joules per kilogram-Celsius.
After some algebraic handling, we get this non-homogeneous first order differential equation:
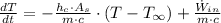
 (Ec. 2)
(Ec. 2)
If we know that
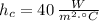 ,
,
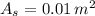 ,
,
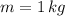 ,
,
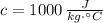 ,
,
 and
and
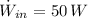 , the differential equation is:
, the differential equation is:
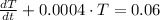
b) The solution of this differential equation is:
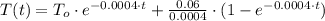
Where
 is the initial temperature of the object, measured in Celsius.
is the initial temperature of the object, measured in Celsius.
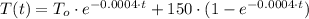

Where
 is the time, measured in seconds.
is the time, measured in seconds.
If we know that
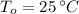 , then:
, then:
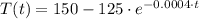 (Ec. 3)
(Ec. 3)
For
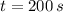 , we get that temperature of the object is:
, we get that temperature of the object is:
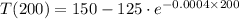
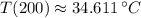
The temperature of the object after 200 second inside the microwave is approximately 34.611 ºC.