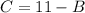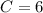Answer:
Algebra 1 = 12 books
Algebra 2 = 5 books
Geometry = 6 books
Explanation:
Given
Represent
Algebra 1 with A
Algebra 2 with B
Geometry with C
For the quantity

To represent the weight, we have that:


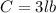

This gives:
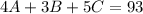
The last sentence in the question can be represented with:

So, the expressions to work with are
 --- (1)
--- (1)
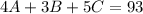 --- (2)
--- (2)
 --- (3)
--- (3)
Substitute A - 1 for B + C in (1)


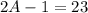
Solve for 2A


Solve for A
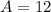
Substitute 12 for A in the (2) & (3)
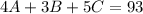
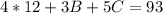
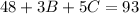
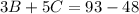
 ---- (4)
---- (4)

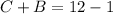
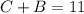
Make C the subject
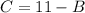 ----- (5)
----- (5)
Substitute 11 - B for C in (4)

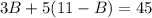
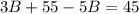
Collect Like Terms
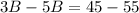
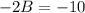
Solve for B


Substitute 5 for B in (5)