Answer:
Reject H₀. There is a significant difference in drug resistance between the two states.
Explanation:
In this case we need to determine whether the data suggest a statistically significant difference between the proportions of drug-resistant cases in the two states.
The significance level of the test is, α = 0.02.
(1)
The hypothesis can be defined as follows:
H₀: There is no difference between the proportions of drug-resistant cases in the two states, i.e.
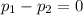 .
.
Hₐ: There is a statistically significant difference between the proportions of drug-resistant cases in the two states, i.e.
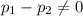 .
.
(2)
Compute the sample proportions and total proportion as follows:
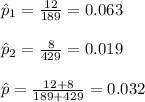
Compute the test statistic value as follows:
![Z=\frac{\hat p_(1)-\hat p_(2)}{\sqrt{\hat p(1-\hat p)* [(1)/(n_(1))+(1)/(n_(2))]}}](https://img.qammunity.org/2021/formulas/mathematics/college/xebev82u5k22fkcmoq6sty9us8je81hyq2.png)
![=\frac{0.063-0.019}{\sqrt{0.032(1-0.032)* [(1)/(189)+(1)/(429)]}}\\\\=2.86](https://img.qammunity.org/2021/formulas/mathematics/college/hsrxt4kolswyvm7z3mhhtgmxatrvvostwz.png)
The test statistic value is 2.86.
(3)
The decision rule is:
The null hypothesis will be rejected if the p-value of the test is less than the significance level.
Compute the p-value as follows:
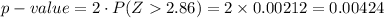
p-value = 0.00424 < α = 0.02.
The null hypothesis will be rejected at 0.02 significance level.
Reject H₀. There is a significant difference in drug resistance between the two states.