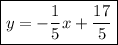Question

Find the equation of the line which passes through the point (7,2) and is perpendicular to y=5x-2

Answer 1

`\displaystyle y=-(1)/(5)x+(17)/(5)`

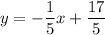
Explanation:

Equation of a line

A line can be represented by an equation of the form

`y=mx+b`

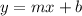
Where x is the independent variable, m is the slope of the line, b is the y-intercept and y is the dependent variable.

We need to find the equation of the line passing through the point (7,2) and is perpendicular to the line y=5x-2.

Two lines with slopes m1 and m2 are perpendicular if:

`m_1.m_2=-1`

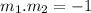
The given line has a slope m1=5, thus the slope of our required line is:

`\displaystyle m_2=-(1)/(m_1)=-(1)/(5)`

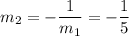
The equation of the line now can be expressed as:

`\displaystyle y=-(1)/(5)x+b`

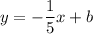
We need to find the value of b, which can be done by using the point (7,2):

`\displaystyle 2=-(1)/(5)*7+b`

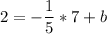
Operating:

`\displaystyle 2=-(7)/(5)+b`

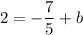
Multiplying by 5:

`10=-7+5b`

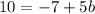
Operating:

`10+7=5b`

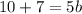
Solving for b:

`\displaystyle b=(17)/(5)`

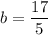
The equation of the line is:

`\boxed{\displaystyle y=-(1)/(5)x+(17)/(5)}`