Answer:
The range of g(x) is [5, ∞) ⇒ (a)
Explanation:
The range of the function is the values of y which corresponding to the values of x (domain)
∵
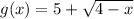
∵ There is no square root for negative values
∴ 4 - x ≥ 0
→ Add x to both sides
∴ 4 - x + x ≥ 0 + x
∴ 4 ≥ x
→ that means x is smaller than or equal to 4
∴ x ≤ 4
→ The greatest value of x = 4
∴ The domain of g(x) = {x : x ≤ 4} ⇒ (-∞, 4]
→ At x = 4
∵ g(4) = 5 +

∴ g(4) = 5 + 0
∴ g(4) = 5
→ That means the smallest value of y = 5 because
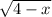 is always
is always
give a positive value which add to 5
∴ The range of g(x) is {y : y ≥ 5} ⇒ [5, ∞)
The right answer is (a)