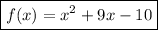Question

Write a quadratic function in standard form with zeros 1 and -10

Answer 1

f(x)=x^2+9x-10

Explanation:

Standard Form of Quadratic Function

The standard form of a quadratic function is:

`f(x)=ax^2+bx+c`

where a,b, and c are constants.

The factored form of a quadratic equation is:

`f(x)=a(x-\alpha)(x-\beta)`

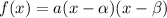
Where
`\alpha` and
`\beta` are the roots or zeros of f, and a is constant.

We know the zeros of the function are 1 and -10. The function is:

`f(x)=a(x-1)(x-(-10))`

`f(x)=a(x-1)(x+10)`

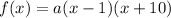
Operating:

`f(x)=a(x^2+10x-x-10)`

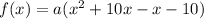
Joining like terms:

`f(x)=a(x^2+9x-10)`

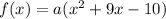
Since we are not given any more restrictions, we can choose the value of a=1, thus. the required function is:

`\boxed{f(x)=x^2+9x-10}`