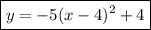Question

Write the equation of the parabola in vertex form.
vertex (4,4), point (3, -1)

Answer 1

`y=-5(x-4)^2+4`

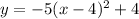
Explanation:

Equation of the Quadratic Function

The vertex form of the quadratic function has the following equation:

`y=a(x-h)^2+k`

Where (h, k) is the vertex of the parabola, and a is a coefficient different from zero.

The vertex is located at (4,4).

Substituting the coordinates of the vertex, the equation of the function is:

`y=a(x-4)^2+4`

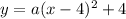
The value of a will be determined by using the given point (3,-1).

`-1=a(3-4)^2+4`

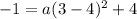
Operating:

`-1=a(1)+4`

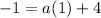
Solving:

`a=-5`

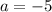
The equation of the graph is:

`\boxed{y=-5(x-4)^2+4}`