Answer:
The ratio of the first term to the common difference is 1 : 2
Explanation:
The rule of the sum of the AP is
![S_(n)=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2021/formulas/mathematics/college/pxwtsxrkkgvi8x38vv0qpvwpbj0uqydi2i.png) , where
, where
a is the first number
d is the common difference
n is the position of the number
∵
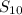 = 4 ×
= 4 ×
 ⇒ (1)
⇒ (1)
→ Find
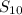 and
and

∵ In
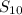 n = 10
n = 10
∴
![S_(10)=(10)/(2)[2a+(10-1)d]](https://img.qammunity.org/2021/formulas/mathematics/college/dfef93xnwsq018oilssly8ti8laquut2kb.png)
∴
![S_(10)=5[2a+9d]](https://img.qammunity.org/2021/formulas/mathematics/college/3e4b1kt0834h4v4b1cc82szujxw1r26rtl.png)
∴
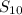 = 10a + 45d ⇒ (2)
= 10a + 45d ⇒ (2)
∵ In
 n = 5
n = 5
∴
![S_(5)=(5)/(2)[2a+(5-1)d]](https://img.qammunity.org/2021/formulas/mathematics/college/tgpxe67osv90bn4bt95qeu9l5t9v505ztg.png)
∴
![S_(5)=2.5[2a+4d]](https://img.qammunity.org/2021/formulas/mathematics/college/6kusw0extd598hat0mzvpmgmcabnb676zk.png)
∴
 = 5a + 10d ⇒ (3)
= 5a + 10d ⇒ (3)
→ Substitute (2) and (3) in (1)
∵ 10a + 45d = 4[5a + 10d]
∴ 10a +45d = 20a + 40d
→ Subtract 40d from both sides
∴ 10a + 45d - 40d = 20a + 40d - 40d
∴ 10a + 5d = 20a
→ Subtract 10a from both sides
∴ 10a - 10a + 5d = 20a - 10a
∴ 5d = 10a
→ Divide both sides by 5
∴ d = 2a
→ That means d is twice a or a is half d
∴ a : d = 1 : 2
The ratio of the first term to the common difference is 1 : 2