Question

Find the value of x .

Answer 1

18

Explanation:

From the given figure, we can see that angle (4x - 11) will be equal to angle 1 since they are corresponding angles

We notice that angle 1 is vertically opposite to angle (2x + 25)

Hence,

angle (4x - 11) = angle 1 = angle (2x + 25)

So, we can say that angle (4x - 11) = angle (2x + 25)

Now, solving for x:

4x - 11 = 2x + 25

2x = 36

x = 18

Answer 2

`x=18`

Explanation:

`(4x-11)\\(2x+25)`

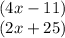
According to the Alternate Exterior Angles Theorem, "when two lines are cut by a transversal, the resulting alternate exterior angles are congruent."

This means that the two expressions above are to be set equal to each other because they are representative of two alternate exterior angles, which are congruent:

`4x-11=2x+25`

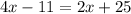
Add
`11` to both sides of the equation:

`4x=2x+36`

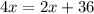
Subtract
`2x` from both sides of the equation:

`2x=36`

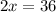
Divide both sides of the equation by the coefficient of
`x`, which is
`2`:

`x=18`

~

Check your work by substituting
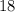`18` for
`x` in the initial equation:

`4(18)-11=2(18)+25`

`61=61`

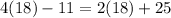
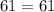
It's correct!